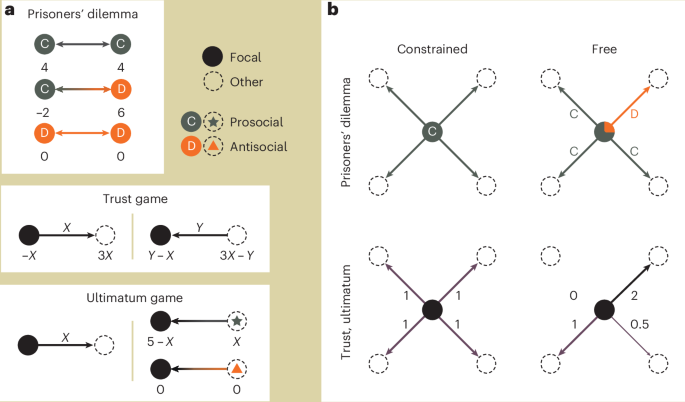
An increase in the proportion of free players in experimental economic games correlates with higher returns in the trust game and greater acceptance rates in the ultimatum game, despite no structural differences between player types in later stages. Each treatment group included three sessions of 49 individuals (N = 147 per group), comparing a control group of constrained players to mixed populations with varying levels of free participants, as well as a fully free-player condition. Box plots display interquartile ranges and medians, while lower panels illustrate effect sizes with 98.75% confidence intervals; statistical significance was assessed via two-sided t-tests adjusted with Bonferroni correction.
Time-series data from three games—prisoner’s dilemma, trust, and ultimatum—show average trends across three replicates, including fitted models with 95% confidence bands (see Extended Data Tables 1 and 2). In the prisoner’s dilemma, cooperation declines slightly in control and mixed conditions but shows a modest rise when all players are free. For the trust game, the amount entrusted decreases slightly in control and extreme free-player density treatments, yet increases under medium density and full freedom. However, the returned amount consistently declines across all conditions. In the ultimatum game, proposed, accepted, and rejected amounts all trend downward regardless of group composition.
Scatter plots present individual outcomes with error bars indicating group means and standard errors. As more free players are introduced, wealth accumulation rises notably among them in both the prisoner’s dilemma and trust game, reflecting strategic adaptability. Inequality patterns vary: in the first two games, inequality spikes when free players are a minority but then declines below initial levels. Conversely, in the ultimatum game, inequality grows with more free players but drops when the population is entirely free, albeit with minor overall fluctuations. Wealth disparities between game stages are significant, particularly in the second stage where most earnings occur. While trust game wealth increases across stages with higher free-player fractions, ultimatum game proposer-stage wealth slightly decreases. Inequality by stage also rises with more free players in both games, suggesting divergent success levels due to strategic optimization.
Using clustering metrics from prior analysis, participants were classified as prosocial, neutral, or antisocial. In the trust game’s second stage, neutral types become more prevalent as free-player比例 rises, contrasting with the first stage where prosocial individuals dominate. Metrics include average returns based on prior receipt (above or below four units) and neighbor behavior. In the ultimatum game’s second stage, patterns mirror the first: neutral players remain stable, prosocial types increase, and antisocial ones decrease. Acceptance behavior is analyzed relative to previous offers and neighboring proposers’ actions.
Regression lines with 95% CIs show that greater freedom enables diverse strategies, evident in data dispersion. Some players entrust less despite higher prior returns from neighbors. Regression slopes range from 0.33 to 0.58, intercepts from 0.25 to 0.63, and adjusted R² values from 0.11 to 0.48, all statistically significant (P < 10⁻¹⁵). In ultimatum game responses, narrow data spread in low-free conditions suggests adherence to successful offers. With more free players, some proposers reduce offers after acceptance, testing responder tolerance. Following rejection, proposers typically raise subsequent offers, indicating learning. Steeper slopes in high-free conditions suggest adaptation to varied responder thresholds. For accepted offers, slopes range from 0.85 to 0.99, intercepts from -0.06 to 0.10, and R² from 0.80 to 0.98. For rejected offers, slopes increase from 0.09 to 0.90, intercepts from 0.30 to 0.71, and R² from 0.02 to 0.39, all significant. --- news from Nature --- News Original --- Social networking agency and prosociality are inextricably linked in economic games Despite the absence of distinction between constrained and free players in the second stage, an increase in the fraction of free players typically results in a rise in (a) the returned amount in the trust game and (b) the accepted amount in the ultimatum game. Each group consisted of three independent sessions with 49 participants per session (N = 147 per group). Each game comprised a control group with a population of constrained players and three treatments with mixed populations, including low, medium, and high fractions of free players, as well as a treatment with a population entirely composed of free players. Upper panels show individual data points, with boxes indicating the 25th and 75th percentiles and the space between the boxes marking the median. Lower panels display effect sizes and 98.75% confidence intervals. Statistical significance was evaluated using two-sided t-tests with the Bonferroni correction. n nThe figure depicts the temporal evolution of six variables across three games, each dataset representing the average of three replicates. The average and the 95% confidence bands of a time series model fitted to the data are also displayed (Extended Data Tables 1 and 2). (a) In the prisoner’s dilemma, the cooperation frequency shows a downtrend in the control group, a slight downtrend in mixed population treatments, and a slight uptrend in the free-player population treatment. (b) In the trust game, the entrusted amount exhibits a slight downtrend in the control and treatments with low and high densities of free players but a slight uptrend in the treatment with a medium density of free players and in the free-player population treatment. The returned amount shows a slight downtrend across both the control and all treatments. (c) In the ultimatum game, the proposed, accepted, and rejected amounts show a downtrend in control and across all treatments. n nScatter plots display individual data points, and the error bars denote the group mean and standard error (SE). Each group consists of three independent sessions with 49 participants per session (N = 147 per group). (a-c) In the prisoner’s dilemma and trust game, wealth based on player type increases steadily as treatments permit more free players. In the ultimatum game, wealth differences are subtle. However, free players are wealthier across all mixed treatment groups, reflecting their ability to optimize strategies for each neighbour. (d-f) In the prisoner’s dilemma and trust game, inequality based on player type initially spikes in the second treatment, where free players are in the minority, and then gradually decreases to levels lower than in the initial treatment. In the ultimatum game, the situation is reversed. Inequality increases with the rising fraction of free players but drops when the population is entirely free, though with smaller variations in overall inequality levels. (g-h) Wealth disparities are more pronounced between stages of the game, as players in both games accrue most of their wealth in the second stage. While in the trust game, wealth consistently increases in both stages as the fraction of free players rises, in the ultimatum game, wealth in the proposer stage slightly decreases with a higher fraction of free players. (i-j) In the trust game, inequality based on game stage increases with a higher fraction of free players, reflecting the fact that more players in the population can optimize their strategies, leading to varying levels of success. In the ultimatum game, inequality increases in both stages, although overall inequality levels remain relatively similar. n nUsing the six clustering factors from Fig. 3, we identify prosocial, neutral, and antisocial types in both stages of the games. a) In the second stage of the trust game, unlike the first stage where prosocial players predominate as the fraction of free players increases, neutral players become more prominent. The clustering factors represent average values in the current round for (A) the returned amount; (B) the returned amount after the trustee received four or more in the previous round; (C) the returned amount after the trustee received less than four in the previous round; and (D - F) the returned amount after up to one, exactly two, or at least three neighbouring trustors sent an amount equal to or greater than in the previous round; b) In the second stage of the ultimatum game, patterns resemble the first stage, with a relatively constant number of neutral players, but an increasing number of prosocial players and a decreasing number of antisocial players. The clustering factors represent average values in the current round for (A) the accepted amount; (B) the accepted amount after receiving a total offer of four or more in the previous round; (C) the accepted amount after receiving a total offer of less than four in the previous round; and (D - F) the accepted amount when up to two, exactly three, or exactly four neighbouring proposers propose an amount equal to or greater than in the previous round. n nEach panel shows fitted regression lines with shaded bands representing 95% confidence intervals (CI). The presence of free players allows for more diverse strategies, observable in the spread of data points. This diversity is evident as some players opt to entrust less despite receiving more from neighbouring trustees in prior rounds. The regression slopes are 0.39 [95%CI: 0.30, 0.48], 0.58 [0.53, 0.63], 0.49 [0.44, 0.54], 0.35 [0.30, 0.39], and 0.33 with [0.28, 0.39], respectively. The intercepts are 0.25 [0.23, 0.28], 0.31 [0.28, 0.34], 0.43 [0.38, 0.47], 0.58 [0.52, 0.63], and 0.63 with [0.56, 0.71], respectively. The adjusted R2 values are 0.11 (F = 72.98, P < 10−15), 0.48 (F = 551.7, P < 10−15), 0.37 (F = 342.2, P < 10−15), 0.30 (F = 255.5, P < 10−15), and 0.19 (F = 140.1, P < 10−15), respectively. n nEach panel shows fitted regression lines with shaded bands representing 95% confidence intervals (CI). The narrow data range in the low fraction of free players’ treatment suggests that proposers adhere to successful offer amounts. In treatments with a majority of free players, some proposers opt to offer less despite previous acceptance, indicating a willingness to test established relationships and adjust responder expectations. However, when offers are rejected, proposers tend to increase their subsequent offers, suggesting they learn from rejection and attempt to make offers more appealing. The steeper slope with higher densities of free players might suggest that in a freer population, proposers encounter a variety of responder thresholds for acceptance, prompting them to adjust their offers upward to find a successful compromise. In the case of acceptance, the regression slopes are 0.85 [95%CI: 0.81, 0.88], 0.99 [0.98, 1.01], 1.00 [0.99, 1.01], 0.98 [0.96, 0.99], and 0.99 [0.98, 1.01], respectively. The intercepts are 0.10 [0.07, 0.13], − 0.02[ − 0.03, − 0.01], − 0.03[ − 0.04, − 0.02], − 0.04[ − 0.06, − 0.02], and − 0.06[ − 0.09, − 0.04], respectively. The adjusted R2 values are 0.80 (F = 2320, P < 10−15), 0.97 (F = 2.11 × 104, P < 10−15), 0.98 (F = 2.74 × 104, P < 10−15), 0.95 (F = 1.14 × 104, P < 10−15), and 0.96 (F = 1.45 × 104, P < 10−15), respectively. In the case of rejection, the regression slopes are 0.09 [95%CI: 0.03, 0.15], 0.27 [0.19, 0.35], 0.58 [0.51, 0.66], 0.47 [0.36, 0.58], and 0.90 [0.80, 1.00], respectively. The intercepts are 0.71 with [0.68, 0.75], 0.59 with [0.55, 0.63], 0.42 with [0.38, 0.47], 0.47 with [0.42, 0.53], and 0.30 with [0.24, 0.37], respectively. The adjusted R2 values are 0.02 (F = 10.16, P < 0.01), 0.09 (F = 46.86, P < 10−10), 0.33 (F = 239, P < 10−15), 0.13 (F = 69.18, P < 10−15), and 0.39 (F = 311, P < 10−15), respectively.